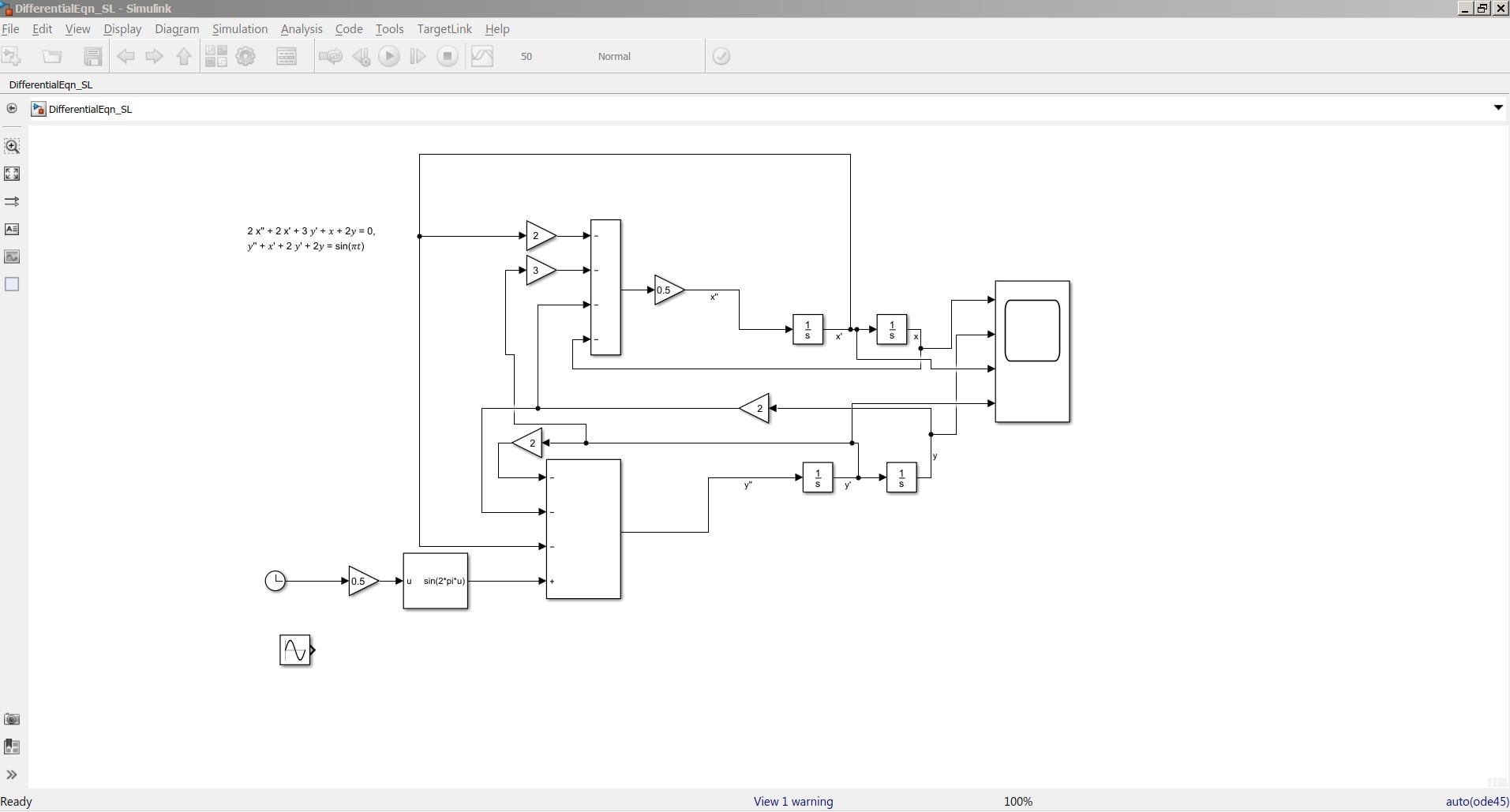
This video shows the steps to design a differential equation 2nd order in Simulink using basic blocks in Matlab 2017b.
Differential Equation in Simulink
2 x” + 2 x’ + 3 ?’ + ? + 2? = 0,
?” + ?’ + 2 ?’ + 2? = sin(??)
Initial Conditions
?'( 0 )= ?1
y( 0 )= 1
x” = -1/2 ( 2 x’ + 3 ?’ + ? + 2?)
?” = sin(??) – ?’ – 2 ?’ – 2?

We will be glad to hear from you regarding any query, suggestions or appreciations at: programmerworld1990@gmail.com
Top posts/ comments from YouTube channel:
The maximum height ‘h’ achieved by an object thrown with a speed ‘v’ at an angle ‘theta’ is given by h=v(sqr)*sin(theta)(sqr)/2g . Create a table showing the maximum height for the following values of v and theta. v=10 20, in steps of 2 and in steps of 10. Use suitable interpolation function to find ‘h’ corresponds to v=13 & 15 and theta = 55 to 65
